Solving miracle sudokus with z3

Introducing the Miracle Sudoku

You are given a sudoku puzzle with these given digits

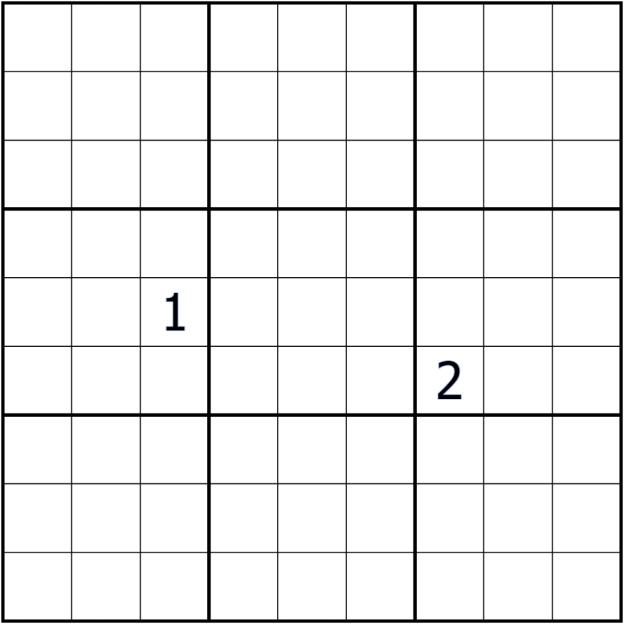
and the following constraints:

All the standard sudoku rules apply
Any two cells separated by a knight's move or a king's move (in chess) cannot contain the same digit
Any two orthogonally adjacent cells cannot contain consecutive digits

Is it possible to solve with a unique solution without resorting to bifurcation (guessing)?

The surprising answer to all-of-the-above is "yes." If you'd like to see the logical deductions a human makes to get there, you can watch the video below:

When I watched the video, I was mesmerized. It was such a beautiful puzzle and required such a spectacular display of logical thinking to work through. Shortly after, I wanted to solve a similar puzzle myself! Unfortunately, there weren't any other instances of this kind of puzzle in the wild (at least, this was true when the video was released).

So, I was stuck.

Or was I?

Computer Science to the Rescue

We're really looking for an instance of this puzzle that can be uniquely solved and has as few clues as possible. Maybe we can write a program to do this for us.

Sometimes it's best to start off with some pseudocode that sketches out the rough idea of what we want to do.

solution := find_any_solution()

for i from 1 to 9x9:
    for each combination of i cells from solution:
        grid := a 9x9 grid only including the cells in combination
        if count_solutions(grid) == 1:
            return grid

Now, let's turn this into actual code. We'll start with the straightforward stuff and hold off (for now) on the more challenging problems.

import itertools

# Find any solution finds a solution to the puzzle using the given starting grid and without matching any of the grids
# in restrictions. It will return the solution grid if there is one, or None if there is no solution.
def find_any_solution(grid, restrictions=[]):
    pass

# Counts the number of unique solutions to the puzzle from the given starting grid.
def count_solutions(grid):
    i = 0
    restrictions = []
    while True:
        solution = find_any_solution(grid, restrictions)
        if not solution:
            return i
        restrictions.append(solution)
        i = i + 1

# Returns an iterable of grids that have a portion of the given solution filled out, ordered by how many cells are given.
def grids_for_solution(solution):
    positions = [(row, col) for row, col in itertools.product(range(9), range(9))]
    for length in range(1, 9 * 9):
        for combo in itertools.combinations(positions, length):
            grid = [[0 for col in range(9)] for row in range(9)]
            for row, col in combo:
                grid[row][col] = solution[row][col]
            yield grid

# Prints the given grid to the console
def print_grid(grid):
    for row in grid:
        print(''.join(str(col) for col in row))

# Creates a puzzle for us
def create_puzzle(restrictions=[]):
    # Find a solution to this puzzle with the given restriction
    solution = [[0 for col in range(9)] for row in range(9)]
    solution = find_any_solution(solution, restrictions)
    
    # Find and print out the puzzle
    for grid in grids_for_solution(solution):
        if count_solutions(grid) == 1:
            print_grid(grid)
            break

Excellent! However, we still need to write the method to find a solution for a given grid. But this should be easy because computers are great at solving sudoku.

Kind of.

Actually, they're pretty bad at it. Sudoku is a classic example of an NP-complete problem where it's fast to check if a solution is correct but slow to find a solution. In the worst case, even a moderately-sized sudoku grid would be out-of-reach for even the world's fastest supercomputers to solve in a reasonable amount of time. But at the grid sizes that humans play at (9x9), it's child's play.

Sudoku is NP-complete, but is that still the case with the new rules?

That's a good question. Indeed, for checking a solved grid, the additional rules are still in P. In the worst case, the puzzle is still NP-complete. It may actually even be easier!

Building the program

Once you know you're stuck on an NP-complete problem, things actually get a bit easier. There are many backtracking algorithms that one can use: one, in particular, is Algorithm X.

However, we're going to take advantage of the fact that the puzzle can be treated as a SAT problem and use the Z3 library.

Basically, we want to describe a bunch of constraints (the rules of our puzzle) to the SAT solver (Z3) and then ask it to find a solution.

With that info, let's start fleshing out the code for find_any_solution.

from z3 import *

# Create solver
s = Solver()

# Create a 9x9 grid of integers
cells = [[Int("%s_%s" % (row+1, col+1)) for col in range(9)] for row in range(9)]

# Every cell contains an integer between 1 and 9
s.add([And(1 <= cells[row][col], cells[row][col] <= 9) for row, col in itertools.product(range(9), range(9))])

Now, we can add the standard Sudoku rules to the solver.

# Row constraints (each cell in a row must contain 1-9 distinctly)
s.add([Distinct(cells[row]) for row in range(9)])
    
# Add column constraints (each cell in a column must contain 1-9 distinctly)
s.add([Distinct([cells[row][col] for row in range(9)]) for col in range(9)])
    
# Add group constraints (each of the 9 3x3 sections must contain 1-9 distinctly)
for row in range(0, 9, 3):
    for col in range(0, 9, 3):
        s.add(Distinct([cells[col+i][row+j] for i, j in itertools.product(range(3), range(3))]))

And, finally, the new rules.

# Cells separated by a king's move (in chess) cannot contain the same digit
king_moves = [(i, j) for i in (-1, 0, 1) for j in (-1, 0, 1) if i != 0 or j != 0]
for row, col in itertools.product(range(9), range(9)):
    moves = [cells[row+i][col+j] for i, j in king_moves if row + i in range(9) and col + j in range(9)]
    s.add(And([cells[row][col] != cell for cell in moves]))

# Cells separated by a knight's move (in chess) cannot contain the same digit
knight_moves = [(i, j) for i in (-2, -1, 1, 2) for j in (-2, -1, 1, 2) if abs(i) + abs(j) == 3]
for row, col in itertools.product(range(9), range(9)):
    moves = [cells[row+i][col+j] for i, j in knight_moves if row + i in range(9) and col + j in range(9)]
    s.add(And([cells[row][col] != cell for cell in moves]))
    
# Orthogonally adjacent cells cannot contain consecutive digits
orthogonal_moves = [(i, j) for i in (-1, 0, 1) for j in (-1, 0, 1) if abs(i) + abs(j) == 1]
for row, col in itertools.product(range(9), range(9)):
    moves = [cells[row+i][col+j] for i, j in orthogonal_moves if row + i in range(9) and col + j in range(9)]
    s.add(And([cells[row][col] - 1 != cell for cell in moves]))
    s.add(And([cells[row][col] + 1 != cell for cell in moves]))

We also want to include the givens from grid in our constraints and exclude the grids given in restrictions.

# The solution has to use our existing grid clues
for row, col in itertools.product(range(9), range(9)):
    if grid[row][col] != 0:
        s.add(cells[row][col] == grid[row][col])

# The solution cannot match our restricted grids
for excluded_grid in restrictions:
    s.add(Not(And(([cells[row][col] == excluded_grid[row][col] for row, col in itertools.product(range(9), range(9))]))))

Finally, we're ready for the solver to find a solution and return it.

# Return the solution
if s.check() != sat:
    return None
result = [[0 for col in range(9)] for row in range(9)]
m = s.model()
for row, col in itertools.product(range(9), range(9)):
    result[row][col] = int(str(m.evaluate(cells[row][col])))
return result

Great! Now, we have everything we need to solve the puzzle.

First, for curiosity's sake, let's find out how many solutions exist to this kind of puzzle.

starting_grid = [[0 for col in range(9)] for row in range(9)]
print(f"There are {count_solutions(starting_grid)} solutions to this puzzle.")

We end up getting 72 total solutions for this puzzle! Not many at all. These rules are very restrictive, as it turns out.

Finally, let's actually generate a puzzle:

# Exclude the original Miracle Sudoku solution
restrictions = [[
    [4, 8, 3, 7, 2, 6, 1, 5, 9],
    [7, 2, 6, 1, 5, 9, 4, 8, 3],
    [1, 5, 9, 4, 8, 3, 7, 2, 6],
    [8, 3, 7, 2, 6, 1, 5, 9, 4],
    [2, 6, 1, 5, 9, 4, 8, 3, 7],
    [5, 9, 4, 8, 3, 7, 2, 6, 1],
    [3, 7, 2, 6, 1, 5, 9, 4, 8],
    [6, 1, 5, 9, 4, 8, 3, 7, 2],
    [9, 4, 8, 3, 7, 2, 6, 1, 5]
]]
create_puzzle(restrictions)

As an example output, we get:

With the rules, there's a unique solution to this puzzle! The question is -- can you solve it? :)

An extra challenge

While Z3 is convenient, it isn't always fast. The program above didn't run very quickly on my machine. Switching from using a 9x9 array of ints to a 9x9x9 array of booleans provided a significant speed boost, and parallelizing the search helped as well.